| N | % | |
|---|---|---|
| Pre-post | 10 | 5% |
| Blocking | 16 | 7% |
| Both | 6 | 3% |
| Neither | 184 | 85% |
Balancing Precision and Retention
in Experimental Design
Gustavo Diaz
Northwestern University
gustavo.diaz@northwestern.edu
gustavodiaz.org
Erin Rossiter
University of Notre Dame
erossite@nd.edu
erossiter.com
Paper and slides: gustavodiaz.org/talk
Bias-variance tradeoff as darts
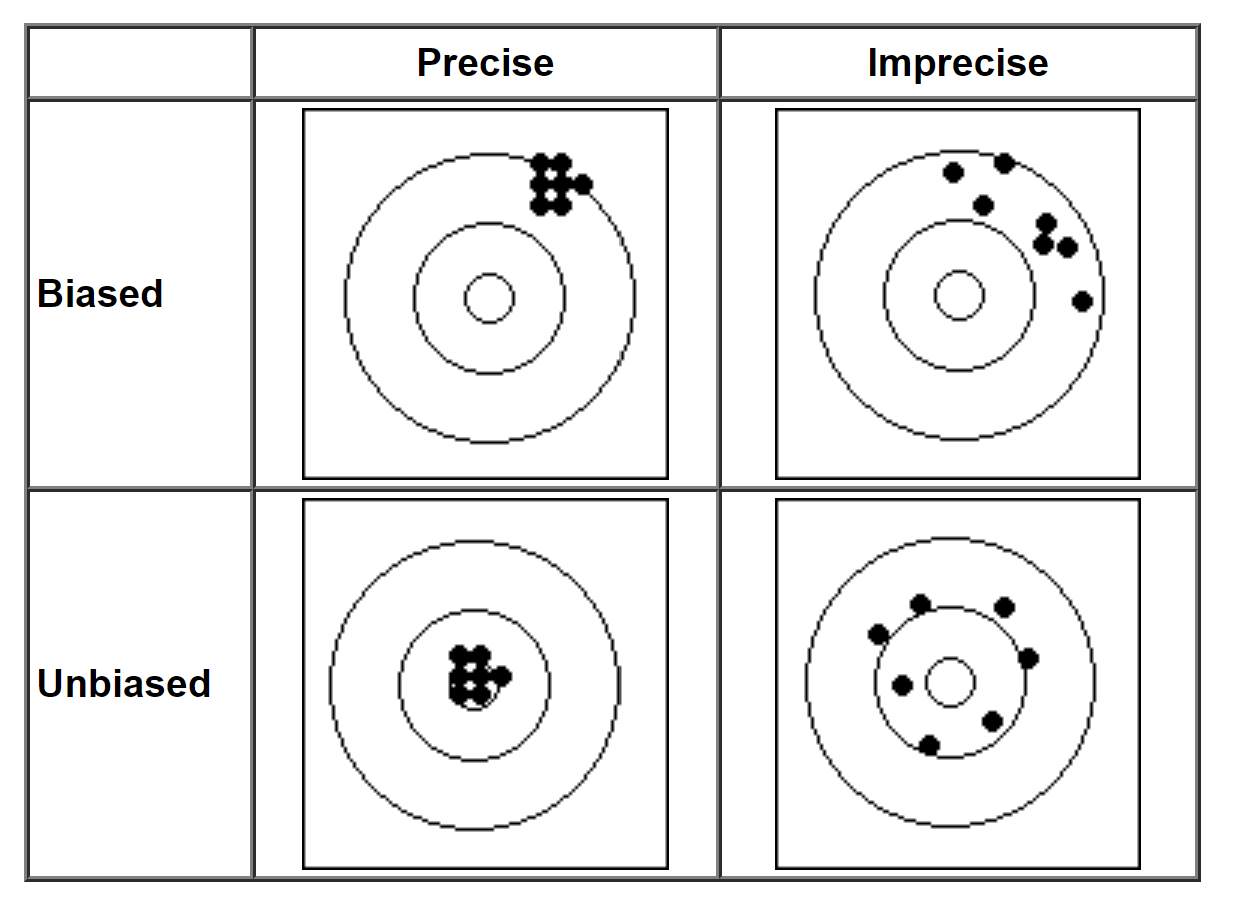
But the game of darts is more complicated
Two types of tradeoffs
Improve precision at the expense of unbiasedness
Improving precision without sacrificing unbiasedness?
Two types of tradeoffs
Improve precision at the expense of unbiasedness
Improving precision without sacrificing unbiasedness?
. . .
Cost has to come from somewhere else!
Improving precision in experiments
. . .
Standard error of estimated ATE in conventional experimental design (Gerber and Green 2012, p. 57)
. . .
\[ SE(\widehat{ATE}) = \sqrt{\frac{\text{Var}(Y_i(0)) + \text{Var}(Y_i(1)) + 2\text{Cov}(Y_i(0), Y_i(1))}{N-1}} \]
\(N\): Sample size
\(Y_i(*)\): Potential outcomes under treatment/control (1/0)
Improving precision in experiments
\[ SE(\widehat{ATE}) = \sqrt{\frac{\text{Var}(Y_i(0)) + \text{Var}(Y_i(1)) + 2\text{Cov}(Y_i(0), Y_i(1))}{N-1}} \]
Improving precision in experiments
\[ SE(\widehat{ATE}) = \sqrt{\frac{\color{#4E2A84}{\text{Var}(Y_i(0)) + \text{Var}(Y_i(1)) + 2\text{Cov}(Y_i(0), Y_i(1))}}{N-1}} \]
. . .
Variance component
Decrease \(SE(\widehat{ATE})\) with alternative research designs
Improving precision in experiments
\[ SE(\widehat{ATE}) = \sqrt{\frac{\color{#4E2A84}{\text{Var}(Y_i(0)) + \text{Var}(Y_i(1)) + 2\text{Cov}(Y_i(0), Y_i(1))}}{N-1}} \]
Variance component
Decrease \(SE(\widehat{ATE})\) with alternative research designs
Block-randomization
Repeated measures
Pre-treatment covariates
Pair-matched design
Online balancing
Sequential blocking
Rerandomization
Matching
Improving precision in experiments
\[ SE(\widehat{ATE}) = \sqrt{\frac{\color{#4E2A84}{\text{Var}(Y_i(0)) + \text{Var}(Y_i(1)) + 2\text{Cov}(Y_i(0), Y_i(1))}}{N-1}} \]
Variance component
Decrease \(SE(\widehat{ATE})\) with alternative research designs
Block-randomization
Repeated measures
Pre-treatment covariates
Pair-matched design
Online balancing
Sequential blocking
Rerandomization
Matching
Improving precision in experiments
\[ SE(\widehat{ATE}) = \sqrt{\frac{\color{#4E2A84}{\text{Var}(Y_i(0)) + \text{Var}(Y_i(1)) + 2\text{Cov}(Y_i(0), Y_i(1))}}{N-1}} \]
Variance component
Decrease \(SE(\widehat{ATE})\) with alternative research designs
Block-randomization
Repeated measures
Pre-treatment covariates
Pair-matched design
Online balancing
Sequential blocking
Rerandomization
Matching
All require pre-treatment information
Improving precision in experiments
\[ SE(\widehat{ATE}) = \sqrt{\frac{\color{#4E2A84}{\text{Var}(Y_i(0)) + \text{Var}(Y_i(1)) + 2\text{Cov}(Y_i(0), Y_i(1))}}{N-1}} \]
Variance component
Decrease \(SE(\widehat{ATE})\) with alternative research designs
Block-randomization
Repeated measures
Pre-treatment covariates
Pair-matched design
Online balancing
Sequential blocking
Rerandomization
Matching
All require pre-treatment information
Two categories:
Reduce variance in observed outcomes
Reduce variance in potential outcomes
Improving precision in experiments
\[ SE(\widehat{ATE}) = \sqrt{\frac{\color{#4E2A84}{\text{Var}(Y_i(0)) + \text{Var}(Y_i(1)) + 2\text{Cov}(Y_i(0), Y_i(1))}}{\color{#00843D}{N-1}}} \]
. . .
Sample size component
Improving precision in experiments
\[ SE(\widehat{ATE}) = \sqrt{\frac{\color{#4E2A84}{\text{Var}(Y_i(0)) + \text{Var}(Y_i(1)) + 2\text{Cov}(Y_i(0), Y_i(1))}}{\color{#00843D}{N-1}}} \]
Sample size component
Quadruple to halve \(SE(\widehat{ATE})\)
. . .
Focus: Increasing numerator may come at the cost of decreasing denominator
. . .
Precision gains from alternative designs may be offset by sample loss
Sample loss
. . .
Explicit
More pre-treatment questions \(\rightarrow\) more attrition/inattention
Block-randomization \(\rightarrow\) discard units
Implicit
Adding a baseline survey \(\rightarrow\) half sample size
Four more survey questions (2 min.) \(\rightarrow\) 72% sample size
. . .
Concerns about prevent widespread implementation
Use of alternative designs to increase precision
Based on articles published in 2022-23 by APSR, AJPS, JOP, PB, CPS, JEPS
Use of alternative designs to increase precision
| N | % | |
|---|---|---|
| Pre-post | 10 | 5% |
| Blocking | 16 | 7% |
| Both | 6 | 3% |
| Mention covariates | 169 | 78% |
| Nothing | 15 | 7% |
Based on articles published in 2022-23 by APSR, AJPS, JOP, PB, CPS, JEPS
Use of alternative designs to increase precision
| N | % | |
|---|---|---|
| Pre-post | 10 | 5% |
| Blocking | 16 | 7% |
| Both | 6 | 3% |
| Mention covariates | 169 | 78% |
| Nothing | 15 | 7% |
Based on articles published in 2022-23 by APSR, AJPS, JOP, PB, CPS, JEPS
Goal
Show that precision gains offset sample loss
. . .
Paper:
Replication of selected studies
Simulation on randomly sampled studies
Simulations/code/advice for pre-analysis stage
Goal
Show that precision gains offset sample loss
Paper:
Replication of selected studies
Simulation on randomly sampled studies
Simulations/code/advice for pre-analysis stage
Replication studies
| Dietrich and Hayes (2023) | Bayram and Graham (2022) | Tappin and Hewitt (2023) | |
|---|---|---|---|
| Study | 1 (DH) | 2 (BG) | 3 (TH) |
| Subfield | AP | IR | AP |
| Topic | Race and issue-based symbolism | Support for IO foreign aid | Party cues and policy opinions |
| Arms | 8 | 5 | 2 |
| Obs. | 515 | 1000 | 775 |
| Waves | 1 | 1 | 2 |
| Concern | Hard to reach population | More precision | Effect persistence |
Replication studies
| Dietrich and Hayes (2023) | Bayram and Graham (2022) | Tappin and Hewitt (2023) | |
|---|---|---|---|
| Study | 1 (DH) | 2 (BG) | 3 (TH) |
| Subfield | AP | IR | AP |
| Topic | Race and issue-based symbolism | Support for IO foreign aid | Party cues and policy opinions |
| Arms | 8 | 5 | 2 |
| Obs. | 515 | 1000 | 775 |
| Waves | 1 | 1 | 2 |
| Concern | Hard to reach population | More precision | Effect persistence |
Replication studies
| Dietrich and Hayes (2023) | Bayram and Graham (2022) | Tappin and Hewitt (2023) | |
|---|---|---|---|
| Study | 1 (DH) | 2 (BG) | 3 (TH) |
| Subfield | AP | IR | AP |
| Topic | Race and issue-based symbolism | Support for IO foreign aid | Party cues and policy opinions |
| Arms | 8 | 5 | 2 |
| Obs. | 515 | 1000 | 775 |
| Waves | 1 | 1 | 2 |
| Concern | Hard to reach population | More precision | Effect persistence |
Replication studies
| Dietrich and Hayes (2023) | Bayram and Graham (2022) | Tappin and Hewitt (2023) | |
|---|---|---|---|
| Study | 1 (DH) | 2 (BG) | 3 (TH) |
| Subfield | AP | IR | AP |
| Topic | Race and issue-based symbolism | Support for IO foreign aid | Party cues and policy opinions |
| Arms | 8 | 5 | 2 |
| Obs. | 515 | 1000 | 775 |
| Waves | 1 | 1 | 2 |
| Concern | Hard to reach population | More precision | Effect persistence |
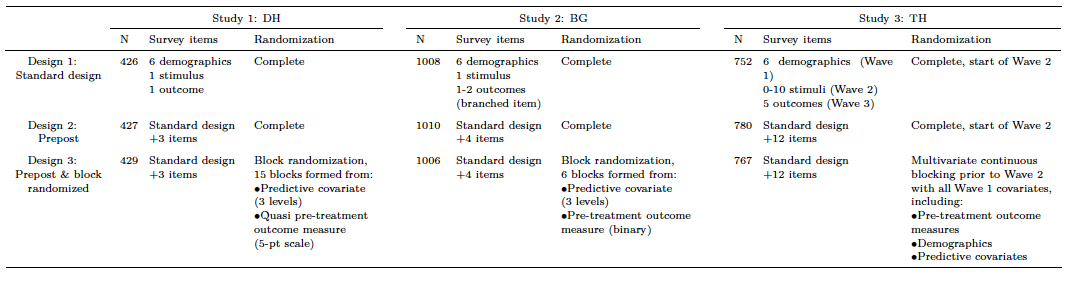
Experimental conditions
| Condition | Outcomes | Randomization |
|---|---|---|
| Design 1 | Post only | Complete |
| Design 2 | Pre-post | Complete |
| Design 3 | Pre-post | Blocking |
- Sample size same as original
- Increased length (DH: 43%, BG: 50%, TH: 110%)
. . .
Evaluate extent of explicit/implicit sample loss
See more here
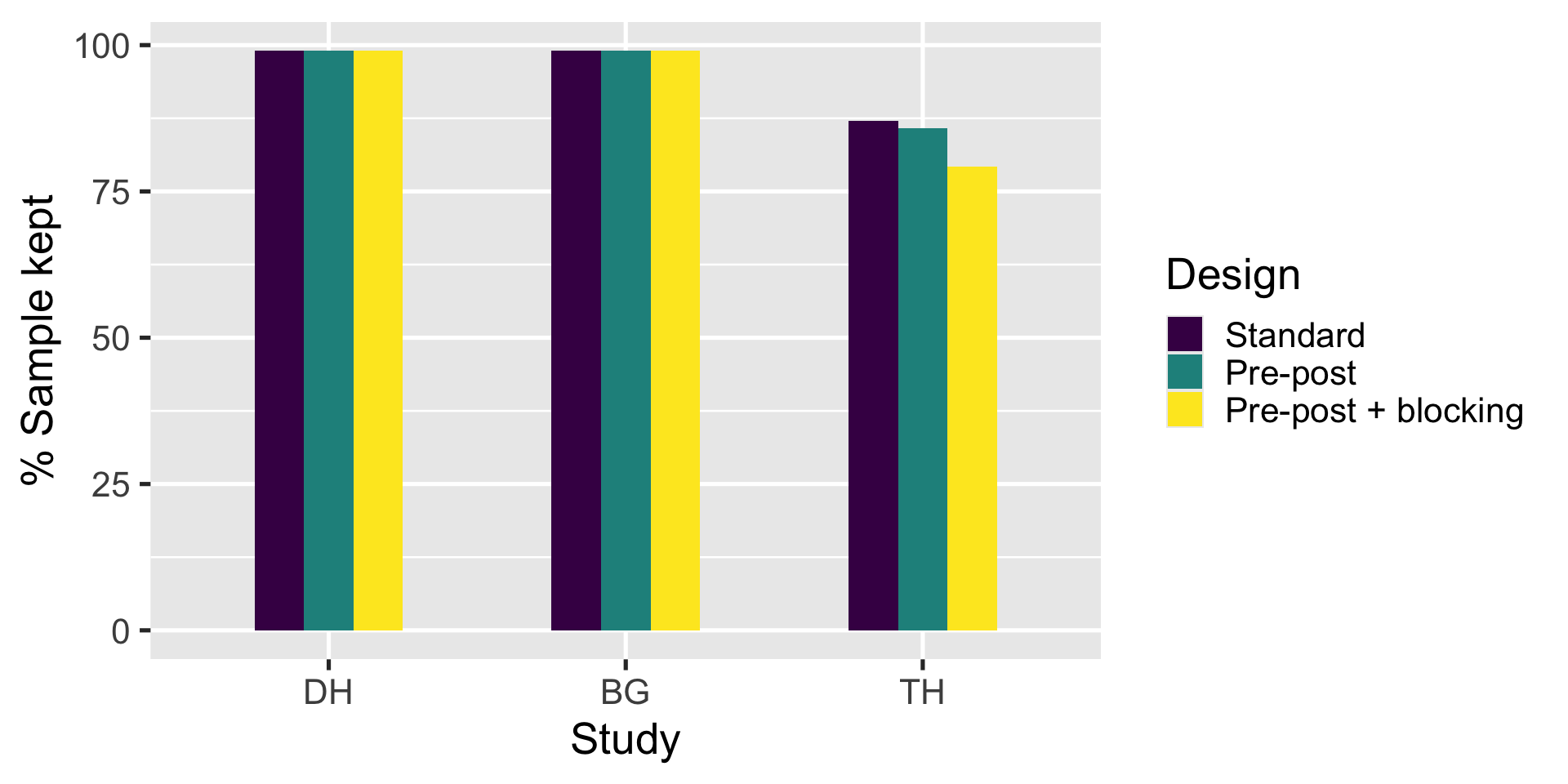
Explicit sample loss
Explicit sample loss
Implicit sample loss
Implicit sample loss
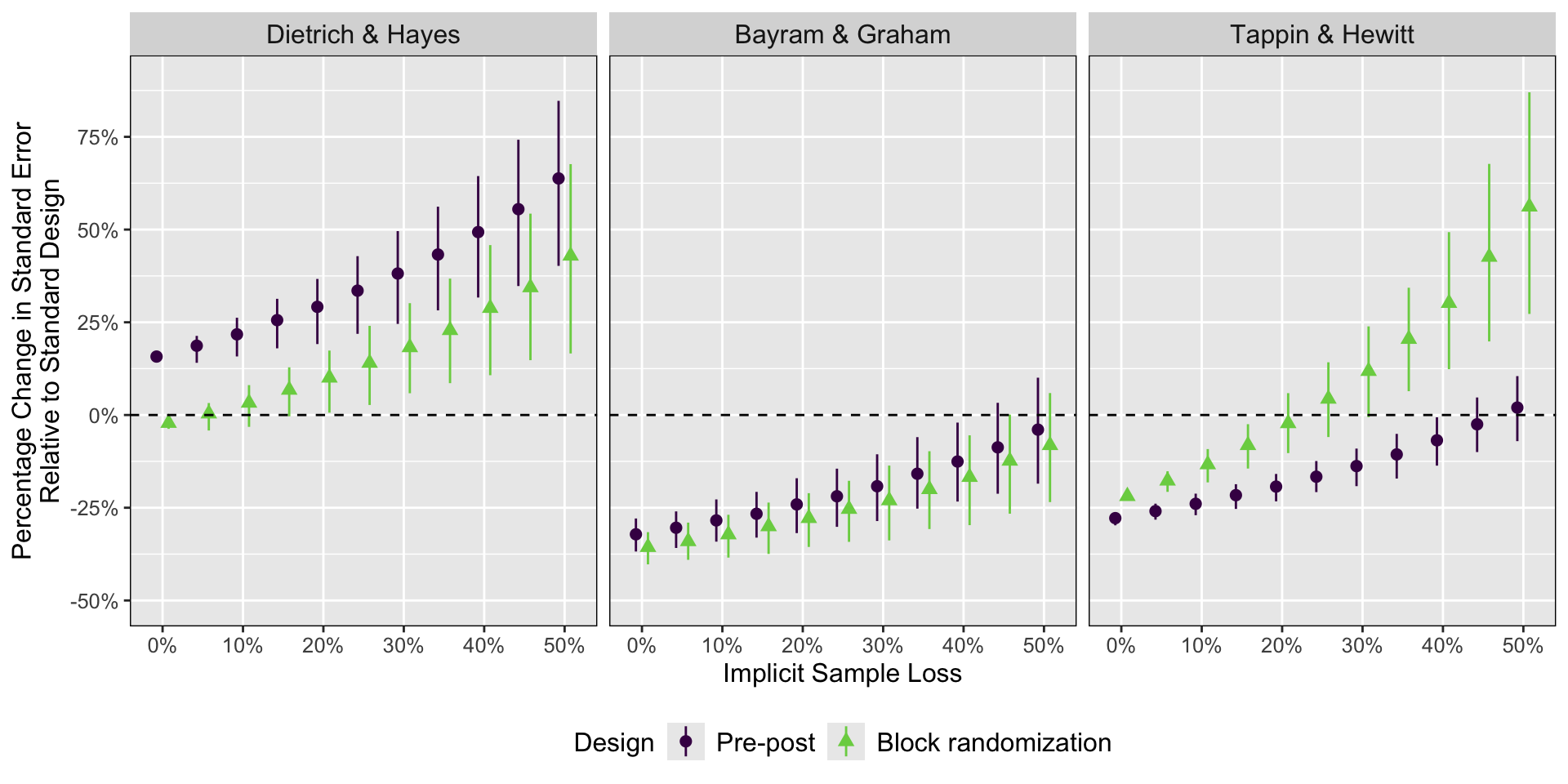
Implicit sample loss
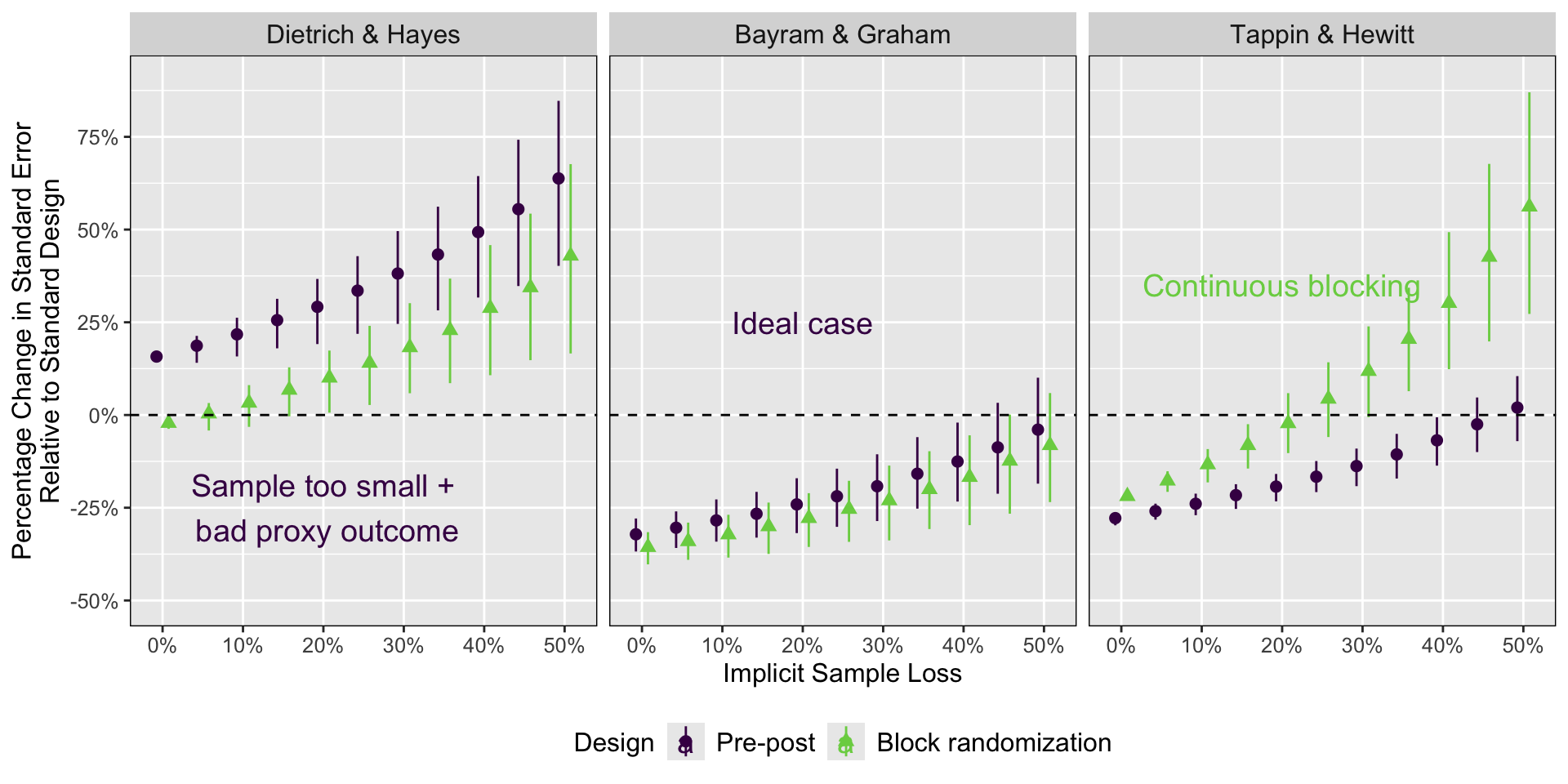
Also in the paper
- No evidence of sample loss altering treatment effects
- No evidence of alternative designs changing sample composition
- Simulated replications point in the same direction
- Ideas to navigate choice at pre-analysis stage
Summary
Puzzle: Alternative designs rare
Argument: Concerns about explicit/implicit sample loss offsetting precision gains
Findings: Alternative designs withstand sample loss
Wrinkle: Alternative designs require more attention!
Takeaway: Try alternative designs!
Paper and slides: gustavodiaz.org/talk
Implementation details